Dave's Math Tables: Integral tanh(x)

(Math | Calculus | Integrals | Table Of | tanh x)

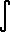Discussion of tanh x dx = ln (cosh x) + C.

1. Proof

Strategy: Use definition of tanh; Use Substitution.

tanh x =

sinh x  cosh x

=

(ex - e-x) / 2  (ex + e-x) / 2

 

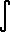tanh x dx =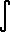

ex - e-x  ex + e-x

dx

set
  u = e^x + e^-x
then we find
  du = (e^x - e^-x) dx

substitute du= (e^x - e^-x) dx, u = e^x + e^-x
 

=

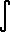du  u

solve

= ln |u| + C

substitute back u = e^x + e^-x

= ln |e^x + e^-x| + C

since e^x and e^-x are always positive

= ln (e^x + e^-x) + C

since (e^x + e^-x)/2 = cosh(x)

= ln (2 cosh x) + C
= ln 2 + ln (cosh x) + C

ln 2 is merely a constant that can be combined with C

= ln (cosh x) + C
Q.E.D.