Dave's Math Tables: Integral coth(x)

(Math | Calculus | Integrals | Table Of | coth x)

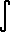Discussion of coth x dx = ln |sinh x| + C.

1. Proof

Strategy: Use definition of coth; Use Substitution.

coth x =

cosh x  sinh x

=

(ex + e-x) / 2  (ex - e-x) / 2

 

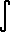coth x dx =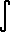

ex + e-x  ex - e-x

dx

set
  u = e^x - e^-x
then we find
  du = (e^x + e^-x) dx

substitute du= (e^x + e^-x) dx, u = e^x - e^-x
 

=

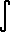du  u

solve

= ln |u| + C

substitute back u = e^x - e^-x

= ln |e^x - e^-x| + C

since (e^x - e^-x)/2 = sinh(x)

= ln |2 sinh x| + C
= ln 2 + ln |sinh x| + C

ln 2 is merely a constant that can be combined with C

= ln |sinh x| + C
Q.E.D.